Vibration Analysis
Characteristics: | KLIPPEL R&D System |
|---|---|
| Accumulated acceleration level AAL | SCN |
| Modal analysis (natural frequencies, modal loss factor, mode shape) | SCN, RMA, HMA |
| Radial and circumferential modes | SCN |
| Rocking modes | SCN, RMA |
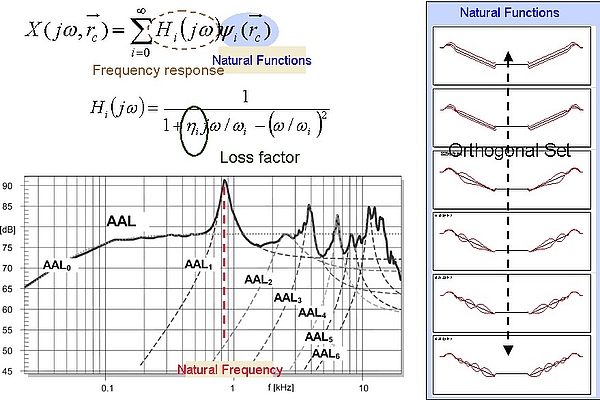
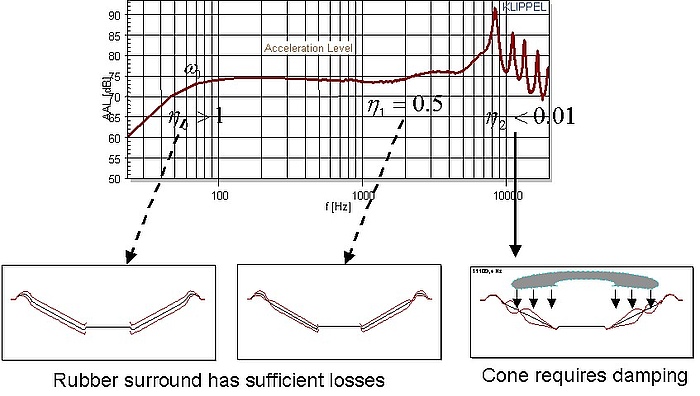
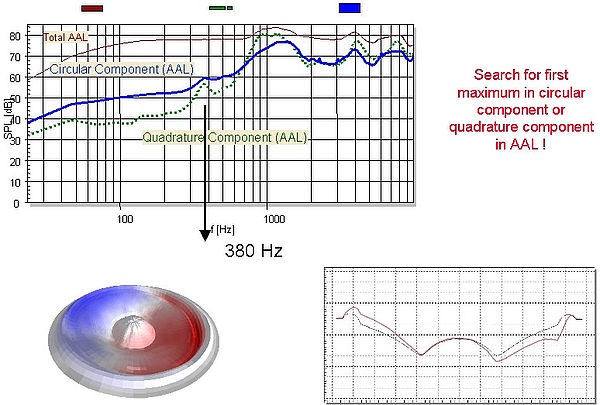
The transfer function Hc(jω, φ, rc) and geometry measured by laser scanning at points r with sufficient resolution on the radiator’s surface are the basis for a mechanical analysis. The figure below shows the principle of modal analysis performed on the loudspeaker cone using the accumulated acceleration level AAL which summarizes the total mechanical vibration on the radiator. The AAL is identical with the SPL at low frequency where the radiator vibrates as a rigid body.
The natural frequencies, the loss factor and the mode shape propagating in radial and circumferential direction are the basis for diagnostics (e.g. finding rocking modes) and practical improvements (e.g. applying additional damping and changing the material and geometry).
KLIPPEL R&D SYSTEM (development)
Module | Comment |
|---|---|
| Scanning Vibrometer System (SCN) | The mechanical analysis can be performed by the SCN as post processing without hardware components (only dongle required). |
| Higher Modal Analysis (HMA) | User laser scanner measurement for automatic identification of modal parameters (modal resonance frequency, damping, gain) and characteristic vibration patterns (mode shapes). This divides the complicated vibration pattern on the diaphragm into separate vibration components that are easier to interpret. Interaction of modes and their influence on sound radiation and response can be studied and non-beneficial vibration-patterns identified. Modal parameters can be used to tune finite element models which share the same "modal view". |
Uses laser scanner vibrometer measurements of transducers for automatic identification of the root-causes of rocking modes. Quantifies imbalances of mass, stiffness and force factor and reveals the location of each imbalance center on the diaphragm. This is useful in avoiding driver instability, voice-coil rubbing and impulsive distortion and in assuring constistency of production. Especially suited for microspeakers and headphone transducers. |
Templates of KLIPPEL Products
TRF Scanning Cone Vibration
Manual scanning of cone vibration using a laser sensor with high cut-off frequency (>15 kHz)
Application Notes
Standards
Audio Engineering Society
AES2 Recommended practice Specification of Loudspeaker Components Used in Professional Audio and Sound Reinforcement
International Electrotechnical Commission
IEC 60268-5 Sound System Equipment, Part 5: Loudspeakers
Other Related Tests
Typical Test Objects
Papers and Preprints
W. Klippel, et al., “Distributed Mechanical Parameters of Loudspeakers Part 1: Measurement,” J. of Audio Eng. Soc. 57, No. 9, pp. 500-511 (2009 Sept.).
W. Klippel, et al., “Distributed Mechanical Parameters of Loudspeakers Part 2: Diagnostics,” J. of Audio Eng. Soc. 57, No. 9, pp. 696-708 (2009 Sept.).
F. J. M. Frankort, “Vibration Patterns and Radiation Behavior of Loudspeaker Cones,” J. of Audio Eng. Soc., Volume 26, No. 9, pp. 609-622 (September 1978).
J. R. Wright, “Automatic Vibration Analysis by Laser Interferometry,” presented at the 88th Convention of the Audio Eng. Soc., Preprint 2889, (March 1990).
A. J. M. Kaizer, “Theory and Numerical Calculation of the Vibration and Sound Radiation of Cone and Dome Loudspeakers with Non-Rigid Diaphragms,” presented at the 62nd Convention of the Audio Eng. Soc., March 1979, Preprint 1437.
C. Struck, “Analysis of the Nonrigid Behavior of a Loudspeaker Diaphragm using Modal Analysis,” presented at 86th convention of Audio Eng. Soc., Hamburg, Preprint 2779 (1989).
A. Chaigne, et al., “On the Influence of the Geometry on Radiation Electrodynamic Loudspeakers,” presented at the 120th Convention of the Audio Eng. Soc., (May 2006), Preprint 6775.
P. J. Anthony, et al., “Finite-Element Analysis in the Design of High-Quality Loudspeakers,” presented at the 108th Convention of the Audio Eng. Soc., February 2000, Preprint 5162.
M. Karjalainen, et al., “Comparison of Numerical Simulation Models and Measured Low-Frequency Behavior of a Loudspeaker,” presented at the 104th Convention of the Audio Eng. Soc., May 1998, Preprint 4722.
J. Wright, “Finite Element Analysis as a Loudspeaker Design Tool,” Paper MAL-11; Conference: AES UK Conference: Microphones & Loudspeakers, The Ins & Outs of Audio (MAL), March 1998.
H. Vollesen, “Control of Loudspeaker Directivity by Mechanical Optimization of the Diaphragm,” presented at the 94th Convention of the Audio Eng. Soc., March 1993, Preprint 3528.
S. Morita, “Acoustic Radiation of a Horn Loudspeaker by the Finite Element Method - A Consideration of the Acoustic Characteristic of Horns,” J. of Audio Eng. Soc., Volume 28, No. 7/8, pp. 482-489, July 1980.
A. Kaizer, “Calculation of the Sound Radiation of a Nonrigid Loudspeaker Diaphragm Using the Finite-Element Method,” J. of Audio Eng. Soc., Volume 36, No. 7/8, pp. 539-551; July 1988.
A. Bright, “Vibration Behaviour of Single-Suspension Electrodynamic Loudspeakers,” presented at the 109th Convention of the Audio Eng. Soc., (September 2000), Preprint 5213.