KLIPPEL R&D系统 (开发)
模组 | 备注 |
|---|---|
| 扫描振动系统 (SCN) | SCN以后处理的方式执行机械振动分析,不需要硬件 (仅需电子狗)。 |
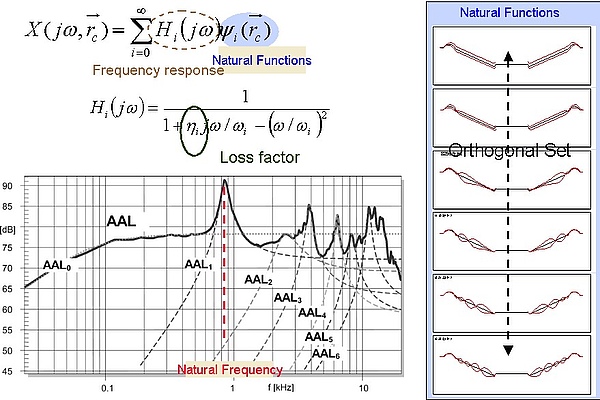
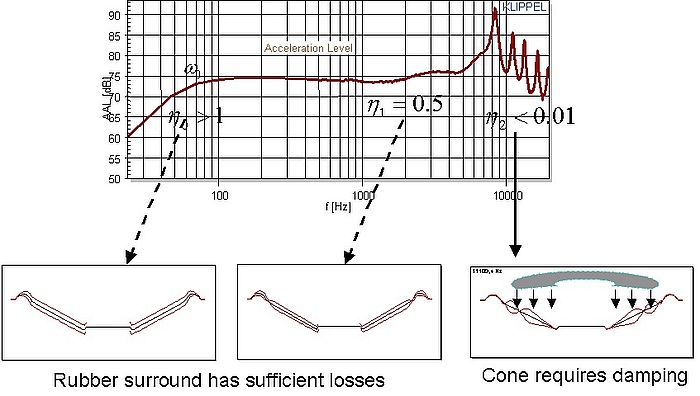
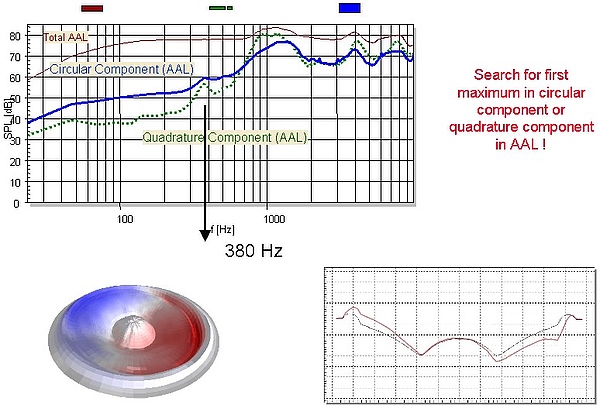
| 高阶模态分析 (HMA) | 使用激光扫描仪进行自动测量识别模态参数(模态共振频率、阻尼、增益)和特征振动模式(模式形状)。这将膜片上复杂的振动模式分为易于理解的单个振动分量,可以研究模式的相互作用及其对声辐射和响应的影响,并可以识别出无益的振动模式。模态参数可用于调整具有相同“模态视图”的有限元模型。 |
使用激光扫描仪进行自动测量识别摇摆模式的根本原因。对质量、刚性和力因数的不平衡进行量化,并揭示每个不平衡中心在振膜上的位置。这在避免驱动单元不稳定、音圈摩擦和脉冲失真以及确保生产一致性方面很有用,特别适用于微型扬声器和耳机换能器。 |
论文和预印本
W. Klippel, et al., “Distributed Mechanical Parameters of Loudspeakers Part 1: Measurement,” J. of Audio Eng. Soc. 57, No. 9, pp. 500-511 (2009 Sept.).
W. Klippel, et al., “Distributed Mechanical Parameters of Loudspeakers Part 2: Diagnostics,” J. of Audio Eng. Soc. 57, No. 9, pp. 696-708 (2009 Sept.).
F. J. M. Frankort, “Vibration Patterns and Radiation Behavior of Loudspeaker Cones,” J. of Audio Eng. Soc., Volume 26, No. 9, pp. 609-622 (September 1978).
J. R. Wright, “Automatic Vibration Analysis by Laser Interferometry,” presented at the 88th Convention of the Audio Eng. Soc., Preprint 2889, (March 1990).
A. J. M. Kaizer, “Theory and Numerical Calculation of the Vibration and Sound Radiation of Cone and Dome Loudspeakers with Non-Rigid Diaphragms,” presented at the 62nd Convention of the Audio Eng. Soc., March 1979, Preprint 1437.
C. Struck, “Analysis of the Nonrigid Behavior of a Loudspeaker Diaphragm using Modal Analysis,” presented at 86th convention of Audio Eng. Soc., Hamburg, Preprint 2779 (1989).
A. Chaigne, et al., “On the Influence of the Geometry on Radiation Electrodynamic Loudspeakers,” presented at the 120th Convention of the Audio Eng. Soc., (May 2006), Preprint 6775.
P. J. Anthony, et al., “Finite-Element Analysis in the Design of High-Quality Loudspeakers,” presented at the 108th Convention of the Audio Eng. Soc., February 2000, Preprint 5162.
M. Karjalainen, et al., “Comparison of Numerical Simulation Models and Measured Low-Frequency Behavior of a Loudspeaker,” presented at the 104th Convention of the Audio Eng. Soc., May 1998, Preprint 4722.
J. Wright, “Finite Element Analysis as a Loudspeaker Design Tool,” Paper MAL-11; Conference: AES UK Conference: Microphones & Loudspeakers, The Ins & Outs of Audio (MAL), March 1998.
H. Vollesen, “Control of Loudspeaker Directivity by Mechanical Optimization of the Diaphragm,” presented at the 94th Convention of the Audio Eng. Soc., March 1993, Preprint 3528.
S. Morita, “Acoustic Radiation of a Horn Loudspeaker by the Finite Element Method - A Consideration of the Acoustic Characteristic of Horns,” J. of Audio Eng. Soc., Volume 28, No. 7/8, pp. 482-489, July 1980.
A. Kaizer, “Calculation of the Sound Radiation of a Nonrigid Loudspeaker Diaphragm Using the Finite-Element Method,” J. of Audio Eng. Soc., Volume 36, No. 7/8, pp. 539-551; July 1988.
A. Bright, “Vibration Behaviour of Single-Suspension Electrodynamic Loudspeakers,” presented at the 109th Convention of the Audio Eng. Soc., (September 2000), Preprint 5213.